POLIEDROS

¿Que es poliedro?

Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico, de la palabra πολύεδρον, de poli muchas y edro caras.

Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topo lógicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topo lógico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como politopos, por lo que podemos definir un poliedro como un polítopo tridimensional.

Elementos de un poliedro

• Caras: Polígonos que limitan al poliedro.
• Aristas: Segmentos intersección de las caras.
• Vértices: Puntos de intersección de las aristas.

Poliedros regulares

Poliedro regular es aquel que cumple:

1. Sus caras son Polígonos regulares iguales.
2. Todos los vértices tienen el mismo orden.

Se llama orden de un vértice de un poliedro, al número de caras (o aristas) que concurren en él.

Sólo existen un total de nueve poliedros regulares diferentes, divididos en dos familias.

1. poliedros regulares Convexos, conocidos como Sólidos platónicos.
2. poliedros regulares Cóncavos, conocidos como Sólidos de Kepler-Poinsot

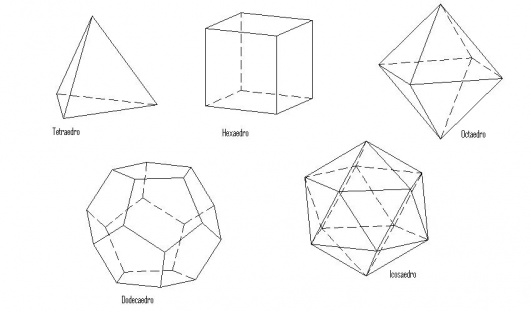
Los sólidos platónicos o sólidos de Platón son poliedros regulares y convexos. Sólo existen cinco de ellos: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro. El nombre del grupo proviene del hecho de que los griegos adjudicaban a estos cuerpos cada uno de los "elementos fundamentales": tierra, agua, aire y fuego, y el restante, el dodecaedro, a la divinidad. Los sólidos platónicos son el inicio del estudio de los poliedros; de estos se derivan los sólidos de Arquímedes y los de Kepler-Poinsot, que a su vez siguen generando más familias.

Los cinco poliedros regulares convexos fueron observados por Platón, quien maravillado por sus propiedades, asoció cada uno de ellos a un "elemento" primigenio de su filosofía (aire, agua, tierra y fuego). Curiosamente, asoció el dodecaedro al "quinto elemento" o ente espiritual de su teoría de la materia. En esta estructura de pensamiento muchos ven la génesis de la teoría molecular, pues muchos elementos cristalinos tienen una estructura atómica que obedece a la forma de tales poliedros.

La combinación de poliedros regulares desarrolla superficies poliédricas que pueden ser aprovechadas en Arquitectura, Ingeniería, Diseño industrial. Estas combinaciones de poliedros regulares son poliedros arquimedianos o el poliedro de catalán.

Figuras de los poliedros regulares convexos

Aplicaciones prácticas

La combinación de poliedros regulares desarrolla superficies poliédricas que pueden ser aprovechadas en arquitectura, ingeniería, diseño industrial

Las combinaciones de poliedros regulares pierden regularidad pero a la vez mantienen varias de las propiedades de los propios poliedros regulares. La mayoría de los poliedros arquimedianos tienen iguales valores angulares, lo que se puede aprovechar para generar empaquetamientos y agregaciones. El sistema poliédrico es tan estable que permite elevar estructuras altas y resistentes con materiales tan ligeros como el Bambú.

La combinación de poliedros regulares se utiliza a menudo en diseño industrial y también en Arquitectura para células constructivas, habitaciones, Mallas espaciales planas, Cúpulas geodésicas, etc., e incluso en épocas anteriores para cúpulas de piedra (bóvedas de crucería renacentistas). Las combinaciones poliédricas también aparecen en la naturaleza, tanto en la estructura de diversos minerales como en elementos estructurales de seres vivos.

El Tetraedro Regular es el punto de partida para Escolleras que necesitan una resistencia especial. El Tetrapodo, cuatro conos de revolución situados desde los vértices hasta el centro de un Tetraedro, se utiliza en las escolleras del norte de Francia desde los años 50 y en las costas de Sudáfrica se usa el Dolos, asimismo conos de revolución dispuestos basándose en la figura del Tetraedro Regular.

La combinación de tetraedros también se ha utilizado en proyectos de arquitectura habitacional que tiene como objetivo la rápida construcción y puesta a punto de viviendas prefabricadas. En Europa se construyó en masa estás células habitacionales, aunque los resultados óptimos se han obtenido en lugares económicamente boyantes como Canadá. Las aplicaciones más primarias formalmente partían del cubo y también se han utilizado en formas tetraédicas u octaédricas.

Las estructuras de base Poliédrica, como la Cúpula Geodésica, sirven en arquitectura para construir estructuras muy livianas y cubrir grandes espacios. Su desarrollo se debe a las investigaciones de Buckminster Fuller en los años 50 y tienen su origen en las estructuras de los Radiolarios Protozoos que habitan en las profundidades marinas.

Las estructuras Reticulares, como la cúpula geodésica, las mallas espaciales planas o las estructuras alabeadas, son estructuras livianas que permiten adaptar su forma a las necesidades de cada proyecto. Se componen de los nudos y las barras, pudiendo ser desmontables y por tanto recuperables. Tienen numerosas aplicaciones en arquitectura, tanto efímera como fija.

Fórmula de Euler

El número de caras más el número de vértices menos el número de aristas es igual a 2.

Sea C el número de caras, V el número de vértices y A el número de aristas se tiene la fórmula.

C + V – A = 2

https://www.ecured.cu/Poliedro_regular
TETRAEDRO
NUMERO DE CARAS: 4
POLÍGONOS QUE FORMAN SUS CARAS: TRIANGULO
ARISTAS: 6 
VÉRTICES: 4 
CARAS CONCURRENTES EN UN VÉRTICE: 4


CUBO
NUMERO DE CARAS: 4
POLÍGONOS QUE FORMAN SUS CARAS: cuadrado
ARISTAS: 12
VÉRTICES: 8 
CARAS CONCURRENTES EN UN VÉRTICE: 3


Octaedro
NUMERO DE CARAS: 8
POLÍGONOS QUE FORMAN SUS CARAS: triangulo
ARISTAS: 12
VÉRTICES: 6 
CARAS CONCURRENTES EN UN VÉRTICE: 4


Dodecaedro
NUMERO DE CARAS: 12
POLÍGONOS QUE FORMAN SUS CARAS: pentágono
ARISTAS: 30
VÉRTICES: 12 
CARAS CONCURRENTES EN UN VÉRTICE: 5

Icosaedro
NUMERO DE CARAS: 20
POLÍGONOS QUE FORMAN SUS CARAS: triangulo
ARISTAS: 30
VÉRTICES: 12 
CARAS CONCURRENTES EN UN VÉRTICE: 5 

TEOREMA DE TALES

EL TEOREMA DE TALES

Autor:

Isamar Promotor, Enrique Hernando Arnáiz

OBJETIVO

• Reconocer el criterio de semejanza de triángulos utilizado en la solución de un ejercicio y problema.
• Identificar el criterio de semejanza de triángulos utilizado para la solución de problemas y ejercicios. 
• Resolver ejercicios relacionados con el Teorema de Thales presentes en la vida cotidiana.

INTRODUCCIÓN: EL teorema de Tales se considera el teorema fundamental de la semejanza de triángulos y establece lo siguiente: Toda recta paralela a un lado de un triángulo, forma con los otros dos lados o con sus prolongaciones otro triángulo que es semejante al triángulo dado.

Aplicaciones del teorema

Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la cuarta y tercera proporcional de dos segmentos dados, la media proporcional, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y razones de segmentos dados, el cálculo de razones simples, razones dobles y cuaternas armónicas, la semejanza y el estudio de las escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones.

Primer teorema de Tales

El Primer Teorema de Tales enuncia que si en un triángulo dado se traza un segmento paralelo a uno de sus tres lados, el nuevo triángulo generado será semejante al primero.

Al triángulo Δ ABC se le traza el segmento A’C’. Vemos que aparece un nuevo triángulo Δ A’BC’ semejante al primero. Tienen sus tres ángulos iguales y sus lados correspondientes son proporcionales.

De acuerdo con el teorema, se verifica que:

Esa razón de proporcionalidad se mantiene entre dos lados de un mismo triángulo y también entre los lados correspondientes del otro.

Otra variante del primer teorema de Tales

Si dos rectas cualquiera (en la imagen: m y n) son cortadas por una serie de rectas paralelas (en la imagen: r, s y t), los segmentos que se forman en una de ellas son proporcionales a los segmentos correspondientes formadas en la otra recta.

Donde se sigue verificando la razón de proporcionalidad que se ha visto en la primera formulación de este teorema:

Esta razón o igualdades determinan a su vez al criterio de paralelismo de rectas.

https://www.universoformulas.com/matematicas/geometria/teorema-tales/

https://www.geogebra.org/m/A9EJgcZq

https://www.ecured.cu/Teorema_de_Tales

TEOREMA DE PITAGORAS

¿Que es el  teorema de Pitágoras?

El teorema de Pitágoras fue nombrado así en honor de Pitágoras de Samos , un matemático que también fue un lider religioso, y creyó que todas las cosas en el universo estaban compuestas de números.

Se supone que él ha sido el primero en probar este teorema acerca de los triángulos rectángulos:

Teorema de Pitágoras . En un triángulo rectángulo con catetos de longitudes a y b e hipotenusa de longitud c , la ecuación siguiente es verdadera:

c ² = a ² + b ²

(Hay muchas formas diferentes de probar esto.)

La hipotenusa de un triángulo rectángulo es el lado opuesto al ángulo recto.

A continuación está una representación grafica. El teorema establece que la suma de las áreas de los cuadrados azul y rojo es igual al área del cuadrado verde.

 

Importante : Recuerde que el teorema de Pitágoras es verdadero solo para triángulos rectángulos – triángulos que tienen un ángulo de 90 ^o .

La conversa del teorema también es verdadera: si un triángulo tiene lados de longitudes a , b , y c , y c ² = a ² + b ² , entonces debe ser un triángulo rectángulo .

Teorema de Pitágoras

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Demostración geométrica del teorema de Pitágoras

Partimos del triángulo rectángulo genérico representado anteriormente para enunciar el teorema. Entonces, construimos un cuadrado cuyo lado mida la suma de los catetos, es decir, un cuadrado de lado  . Estaremos de acuerdo que el área de este cuadrado es 

Hemos puesto las medidas de  y  de tal forma que si trazamos las hipotenusas construimos cuatro triángulos rectángulos como el genérico, quedando un cuadrado interno de lado  .

Ahora podemos escribir el área del cuadrado grande, que antes hemos calculado como  , pero haciendo la suma de las áreas de los cuatro triángulos más el cuadrado interno.

Tenemos cuatro triángulos rectángulos de área  y un cuadrado de área  . Nos queda pues la siguiente igualdad:

Desarrollamos a los dos lados:

Con lo que acabamos de obtener la relación que enuncia el teorema de Pitágoras.

También nos podemos encontrar enunciados del teorema de Pitágoras en los que utilizan otras letras/variables para expresar la igualdad. Así, si llamamos  a la hipotenusa y  y  a los dos catetos nos queda

https://www.geoka.net/triangulos/teoerma_pitagoras.html

https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/pythagorean-theorem

https://www.sangakoo.com/es/temas/teorema-de-pitagoras

 

DISTINTOS TIPOS DE TEOREMAS MATEMÁTICOS

Encontraremos todos los teoremas matemáticos y sus comprobaciones en GeoGebra esto con la finalidad de que encuentres sus características,definición, ejemplos y sus pasos de como hacerlo en GeoGebra. ❤

Esto te ayudara a construir, interpretar modelos matemáticos mediante la aplicación de procedimientos aritméticos, algebraicos, geométricos y la demostración de teoremas matemáticos con el uso de las tic's